Definisi
Dalam geometri, jarak adalah panjang ruas garis terpendek antara dua objek geometri. Pada materi kali ini, kita akan mempelajari jarak antara titik, garis, dan bidang.1. Jarak Antara Dua Titik
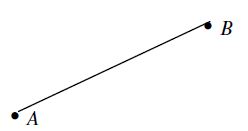
Jarak antara dua titik adalah dengan menarik garis hubung terpendek antara kedua titik tersebut, jadi jarak antara titik A dan B adalah panjang garis AB.
2. Jarak Antara Titik dan Garis
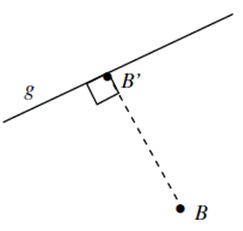
Jarak titik ke garis adalah jarak terdekat sebuah titik ke garis, jarak terdekat diperoleh dengan menarik garis yang tegak lurus dengan garis yang dimaksud. Jarak titik B dengan garis g adalah panjang garis BB’.
3. Jarak Tiitik dengan Bidang
Untuk menentukan jarak sebuah titik pada suatu bidang, maka terlebih dahulu ditarik garis lurus yang terdekat dari titik ke bidang, sehingga memotong bidang dan garis tersebut harus tegak lurus dengan bidang.
Misalkan titik B terletak di luar bidang α maka jarak titik B ke bidang α dapat ditentukan sebagai berikut:
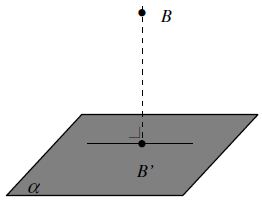
Jarak titik B ke bidang α adalah panjang garis BB’.
4. Jarak Dua Garis Sejajar
Jika ada dua garis yang sejajar, maka jarak kedua garis dengan menarik garis yang tegak lurus dengan kedua garis tersebut.
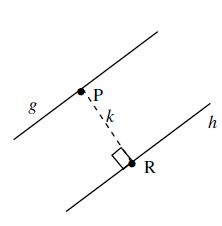
Seperti tampak pada gambar di atas, dimana garis g dan h adalah dua garis yang sejajar, maka jarak kedua garis tersebut adalah garis PR.
5. Jarak Antara Garis dan Bidang yang Sejajar
Untuk mengukur jarak garis ke bidang yang sejajar, maka terlebih dahulu kita tentukan titik sembarang pada garis kemudian kita tarik garis lurus dari titik tersebut ke bidang sehingga garis yang terbentuk tegak lurus terhadapa bidang. Seperti tampak pada gambar di bawah.
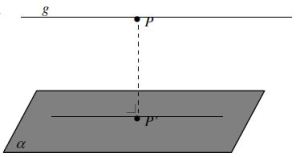
Jarak garis g ke bidang α adalah garik PP’.
6. Jarak Antara Dua Bidang
Untuk mengukur jarak dua bidang, pilihlah sembarang titik pada salah satu bidang kemudian ditarik garik luruh dari titik yang telah ditentukan ke bidang lainya, sehingga garis yang terbentuk tegak lurus terhadap kedua bidang. Seperti tampak pada gambar berikut:
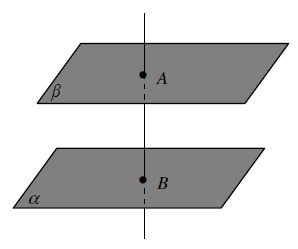
Jarak antara bidang α dan β adalah ruas garis AB.
Contoh
Perhatikan kubus ABCD.EFGH berikut:
Jarak antara titik A dan titik C adalah ruas garis AC
Jarak antara tik E dengan garis CG adalah ruas garis EG
Jarak antara garis AE dengan garis CG adalah ruas garis AC atau EG
Jarak antara titik F dengan bidang ABCD adalah ruas garis FB
Jarak antara bidang BDG dengan AFH adalah ruas garis PQ









